Passing the football has become an increasingly integral part of the NFL.
Intuitively, more passing breeds more interceptions that could change the course of a game. A variety of factors determine how often a quarterback throws interceptions. It can be rationally hypothesized that quarterbacks who throw the ball down the field more often tend to have higher interception rates because deeper throws are less accurate. Inversely, quarterbacks who rarely force the ball down the field will have a lower interception rate — Drew Brees at the end of his career is a great example.
Click here for more PFF tools:
Rankings & Projections | WR/CB Matchup Chart | NFL & NCAA Betting Dashboards | NFL Player Props Tool | NFL & NCAA Power Rankings
Best Bets Tool
While they are shown the same in the stat sheet, not all interceptions are created equal. A hail mary at the end of the game will have a higher chance of being intercepted than an eight-yard pass on first-and-10. This also means interceptions thrown in desperation should be weighted less when calculating a quarterback's interception rate, as it doesn’t really reflect a quarterback’s skill at avoiding turnovers.
Some may argue Aaron Rodgers is a lucky quarterback when it comes to his interception rate. The validity of that is unknown, as of now, unless you continue reading, of course.
In this article, I aim to estimate the interception probability on every passing play since 2014 and determine which quarterbacks are luckier than others.
To model the probability of an interception, I used extreme gradient boosting (XGBoost), which is a package on RStudio. Using this machine learning algorithm, I fit a binary classification model to determine a number between zero and one that estimates the chance a given throw will be intercepted. To model this, I use a variety of situational and performance-based variables.
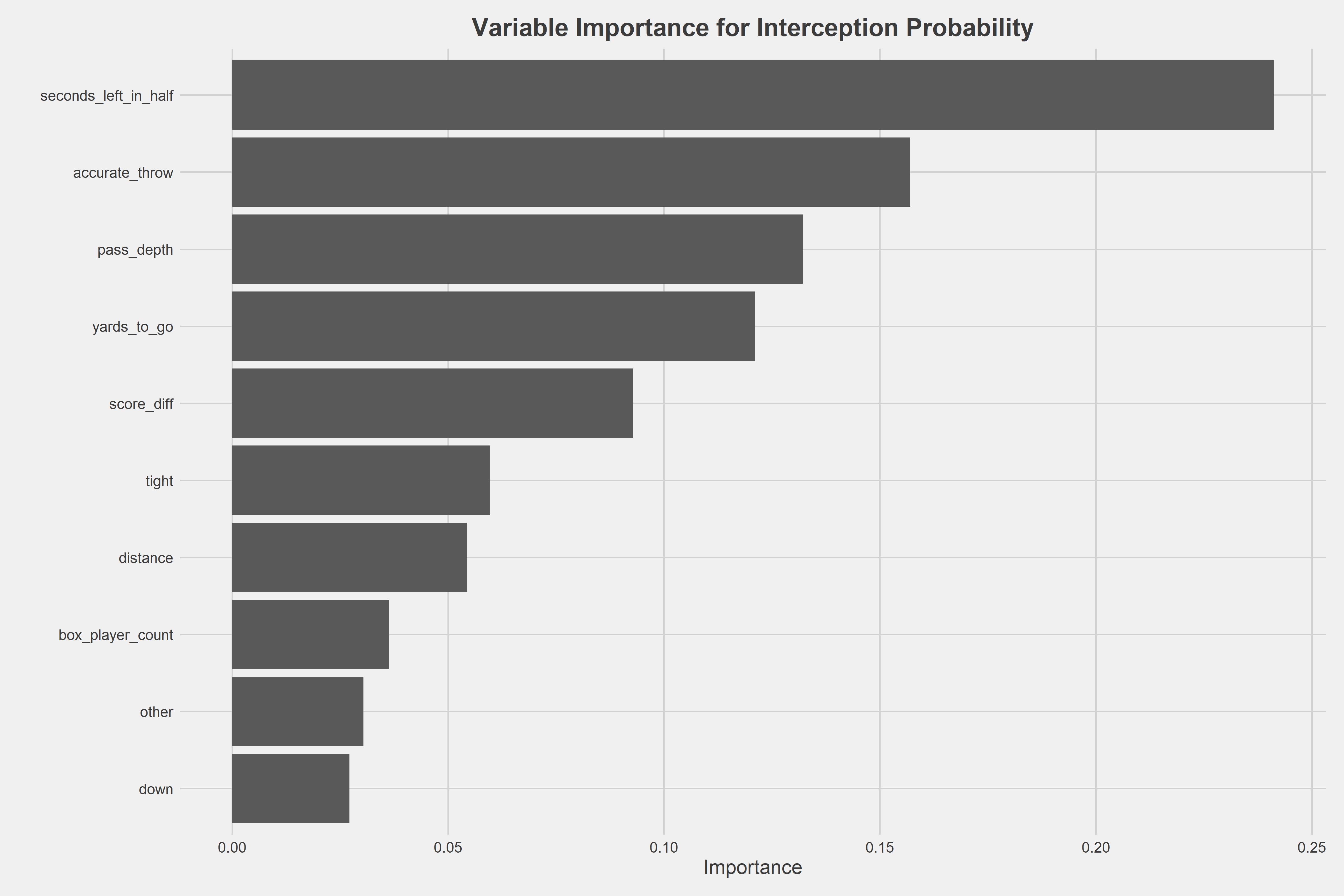
The number of seconds remaining in the half is the most important variable when predicting interceptions, by far. This makes sense, as a big contributor to an interception is desperation. As mentioned earlier, hail marys, or throws of similar type, have high chances of being intercepted. The variable with the second-highest importance is whether or not the throw was accurate. There is a limit to how well we can determine accuracy as of now, though PFF’s charting currently does a great job with that. Additionally, I take into account receiver separation, batted passes and game situations variables such as down, distance and score differential at the time of the throw.
Now that the model has been trained while the predictors were chosen, the next step is to take a look at the distribution of interception probabilities when a throw was picked off.
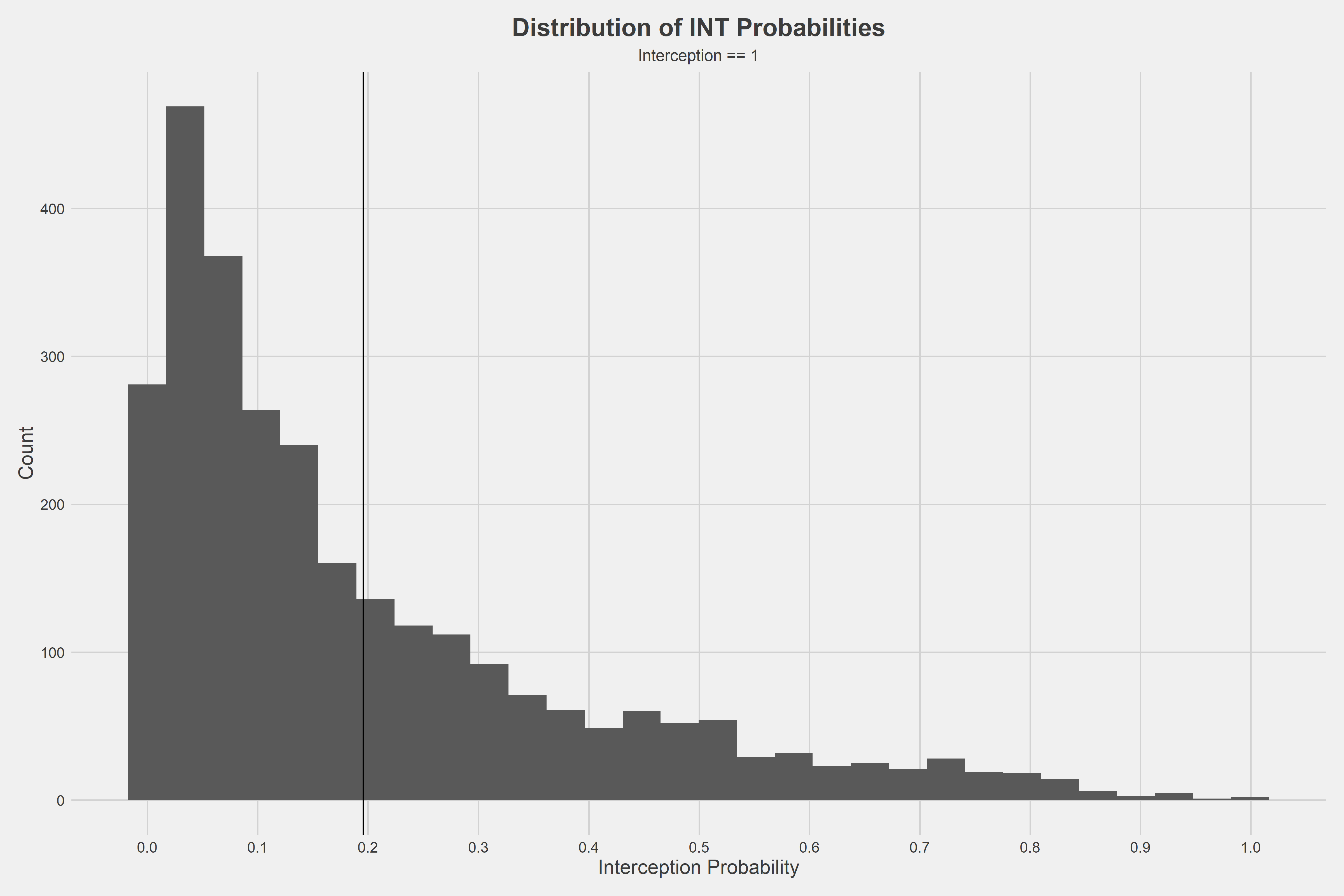
On average, an interception had a 20% chance of being picked off while many interceptions that had very small chances of being picked off were actually intercepted.
If you have a strong enough understanding of modeling, you may be worried about the model overfitting, and due to the number and specificity of variables, that is a completely valid concern. If you make the model too accurate without tuning it, it has a much higher chance of overfitting. What this will do is allow the model to learn too much, which makes it difficult for it to calculate interception probabilities for a new dataset it has never seen before.
However, the model is tuned well, which essentially means through machine learning, the ideal parameters for calculating interception probability were found. When looking at the untuned model’s distribution of interception probabilities on intercepted throws, it showed a U-shaped distribution, which is a sign of overfitting. However, the distribution above is quite nice, as a long right tail shows signs that the model is well-tuned.
The third most important predictor for interception probability is depth of target. Understanding the relationship between depth of target and expected interception probability is key.
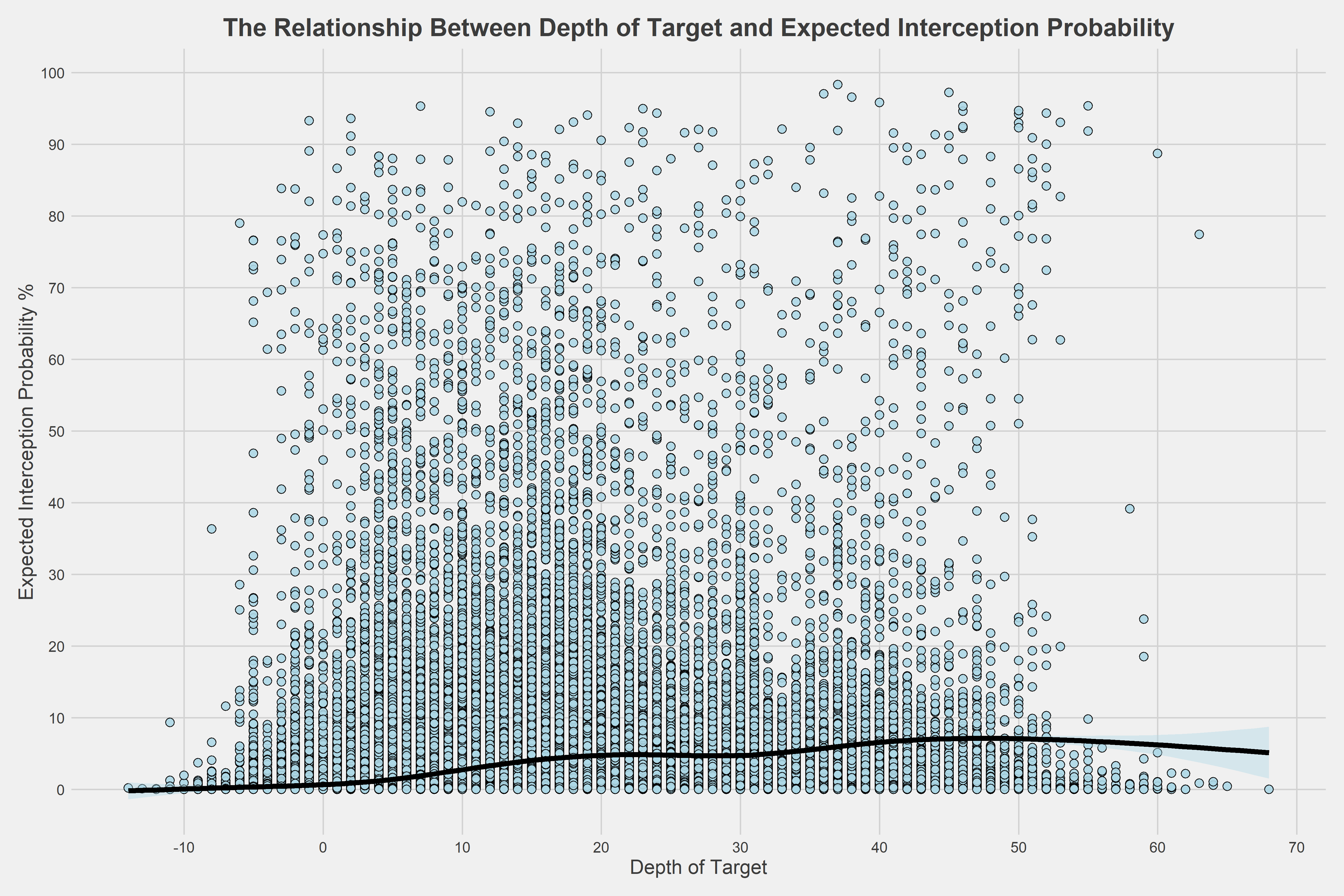
As the depth of a pass increases, its chances of being intercepted increase, which confirms our prior opinion. Though. on average, a 60-yard deep ball only has around an 8% chance of being intercepted, and we can get more accurate than that.
Related content for you:
Does Tom Brady really draw more roughing the passer calls than other quarterbacks? via Conor McQuiston
With this in mind, we can use the third most important predictor, PFF’s charted pass accuracies. The goal of this is to get a better idea of what kind of throws warrant higher and lower chances of interceptions.
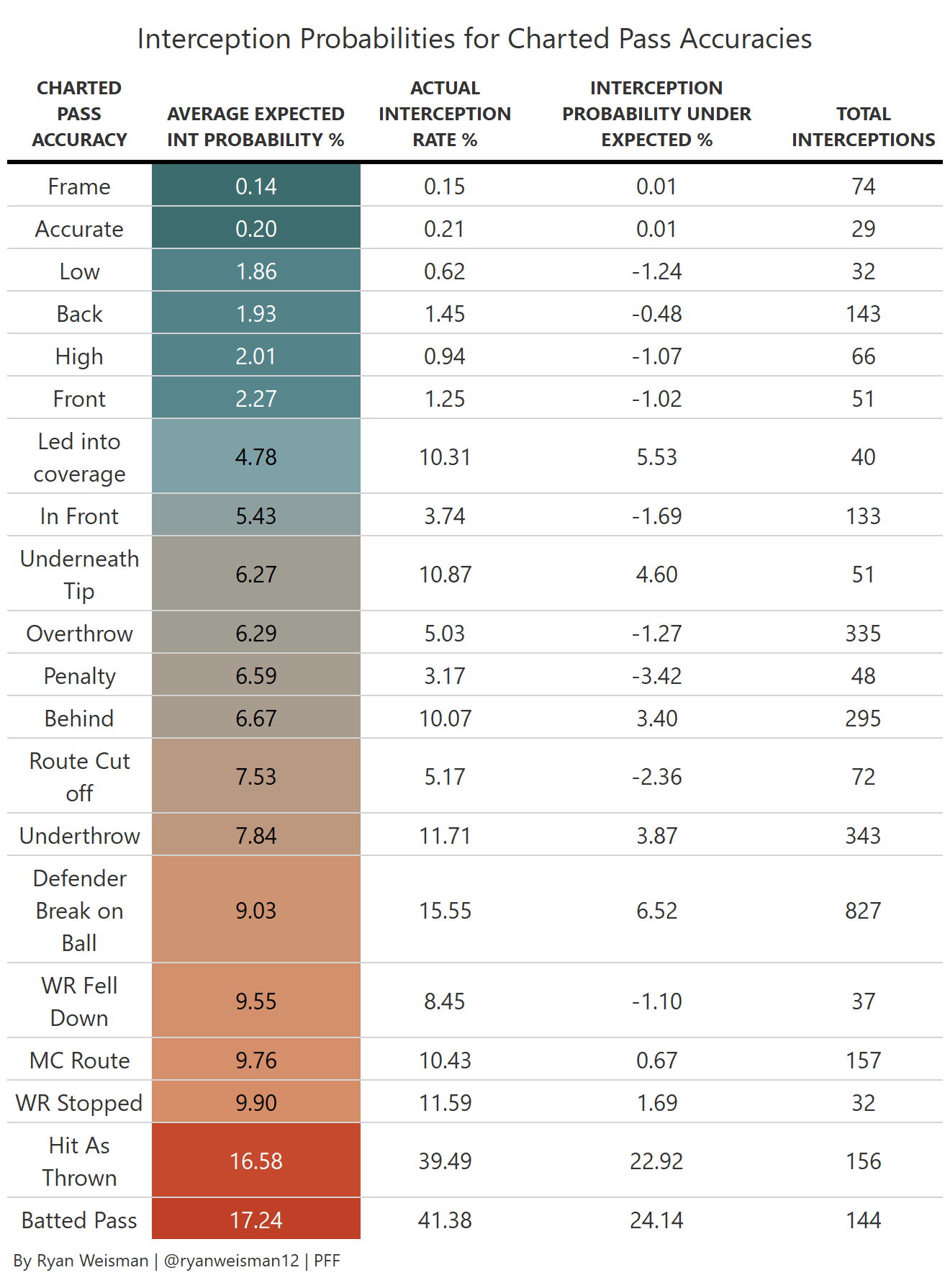
We can see batted passes have the highest chance of being intercepted at around 17%. In actuality, the rate of a batted pass being intercepted is 41%. What this tells us is for events that would greatly affect that trajectory of the ball, such as a batted pass or being hit as thrown, the model suggests the chances of an interception should be a lot lower than it actually is.
Typically, accurate throws have really low chances of being intercepted. Even throws that may be a bit high but are still catchable by the receiver have relatively low chances. The chances increase with more random events, such as batted passes or receivers falling down.
This all circles back to the idea of luck and adjusting for certain magnitudes of interceptions. You don’t want a receiver error interception to be weighted the same as an accurate throw interception when evaluating a quarterback's interception rates. What the model does is adjust for this and weigh these random receiver errors or batted pass events higher. This will be reflected when we look at this metric across quarterbacks later in the article.
We can use this expected interception probability information to create under-expected metrics to determine luck. Due to the model computing the probability of an interception on every single passing play, you can really dig into certain plays and say, “well, that play had only a 5% chance of being intercepted but still was, so the quarterback was unlucky,” or something similar saying, “the quarterback threw a 50-yard bomb into double coverage but the defender dropped the ball, so he’s lucky.” When you take the average of all of these plays, this gives us a large enough sample size to determine accurate under-expected metrics. Taking a look at the film can help understand this better.
Here is the situation for this play:
- 2016 Week 13 – New York Jets vs. Indianapolis Colts
- Third-and-10 | First quarter | 14:11 | 0-0
- 89 yards to go | 13-yard pass | was pressured
- Tight receiver separation | Defender break on ball charted accuracy
This pass had a 90.7% chance of being intercepted, but the ball went right through the defender’s hands, so Ryan Fitzpatrick got lucky.
Here’s another play:
Essentially, Jalen Hurts tosses this ball up into double coverage. It had a 96% chance of being intercepted, and it was.
We now have a pretty good understanding of how the model works and what its uses are. We’ve established it adjusts for desperation and the type of throw, and we’ve had a little film session.
The final thing to do is slightly adjust the average interception probability for a quarterback to make it more accurate, as simply taking the raw average score from all of their plays is not enough. To calculate a quarterback’s expected interception probability within a given period of time, subtract the average expected interception probability for all quarterbacks from the average interception rate for all quarterbacks then add the specific quarterback’s raw average to that subtraction. This allows us to better apply the statistic to evaluating the quarterback as a whole instead of singular plays.
Now, here’s the fun part. Which quarterbacks are luckier than others?
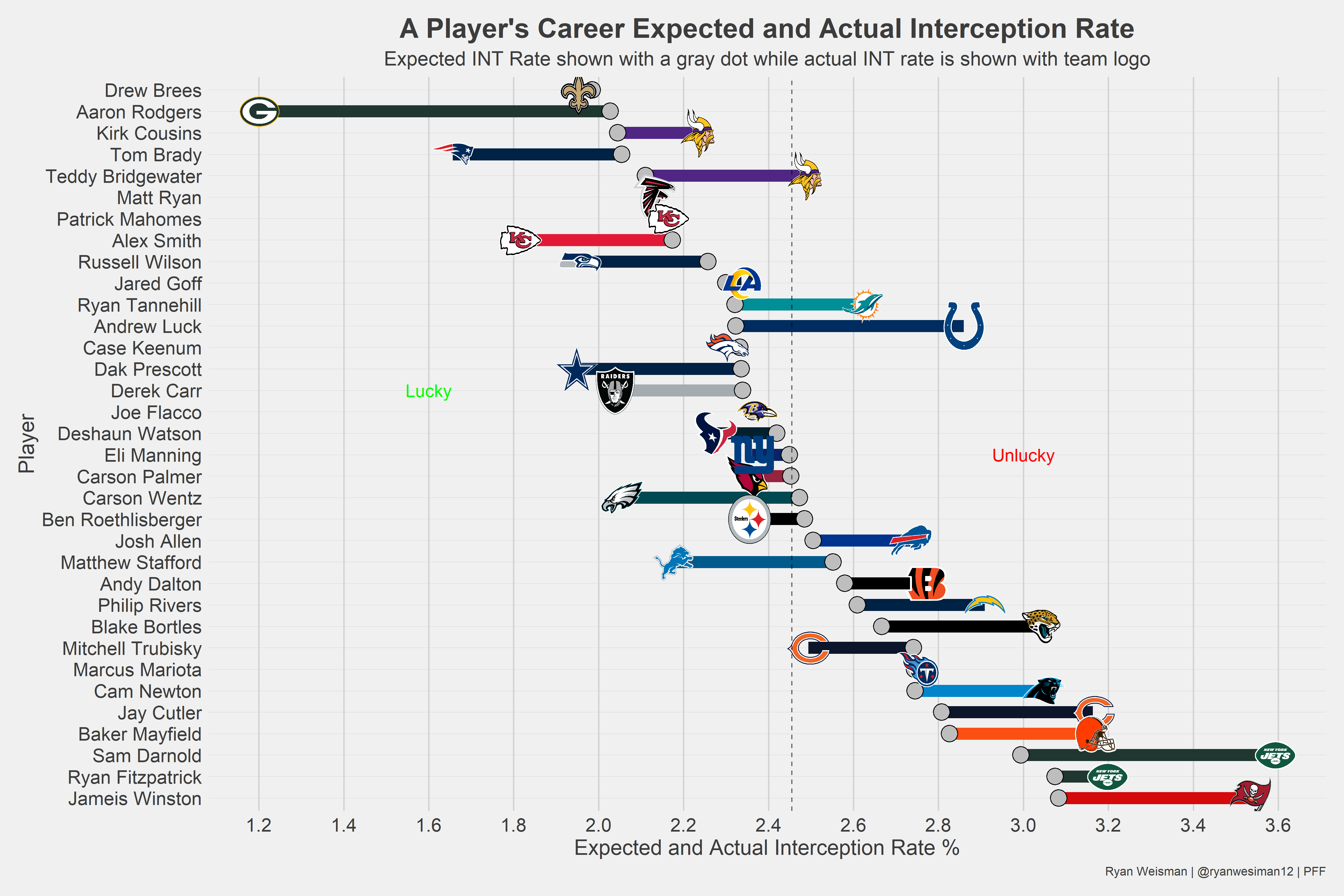
Earlier, I mentioned that many consider Rodgers to be lucky in terms of interceptions. Until now, we couldn’t prove it, as we had no way to quantify it. The only quarterback who has a lower expected interception rate than Rodgers since 2014 is Brees, which can be explained by the fact that Brees has historically been really conservative with his throws while simultaneously being incredibly accurate.
Here’s a better way to look at it.
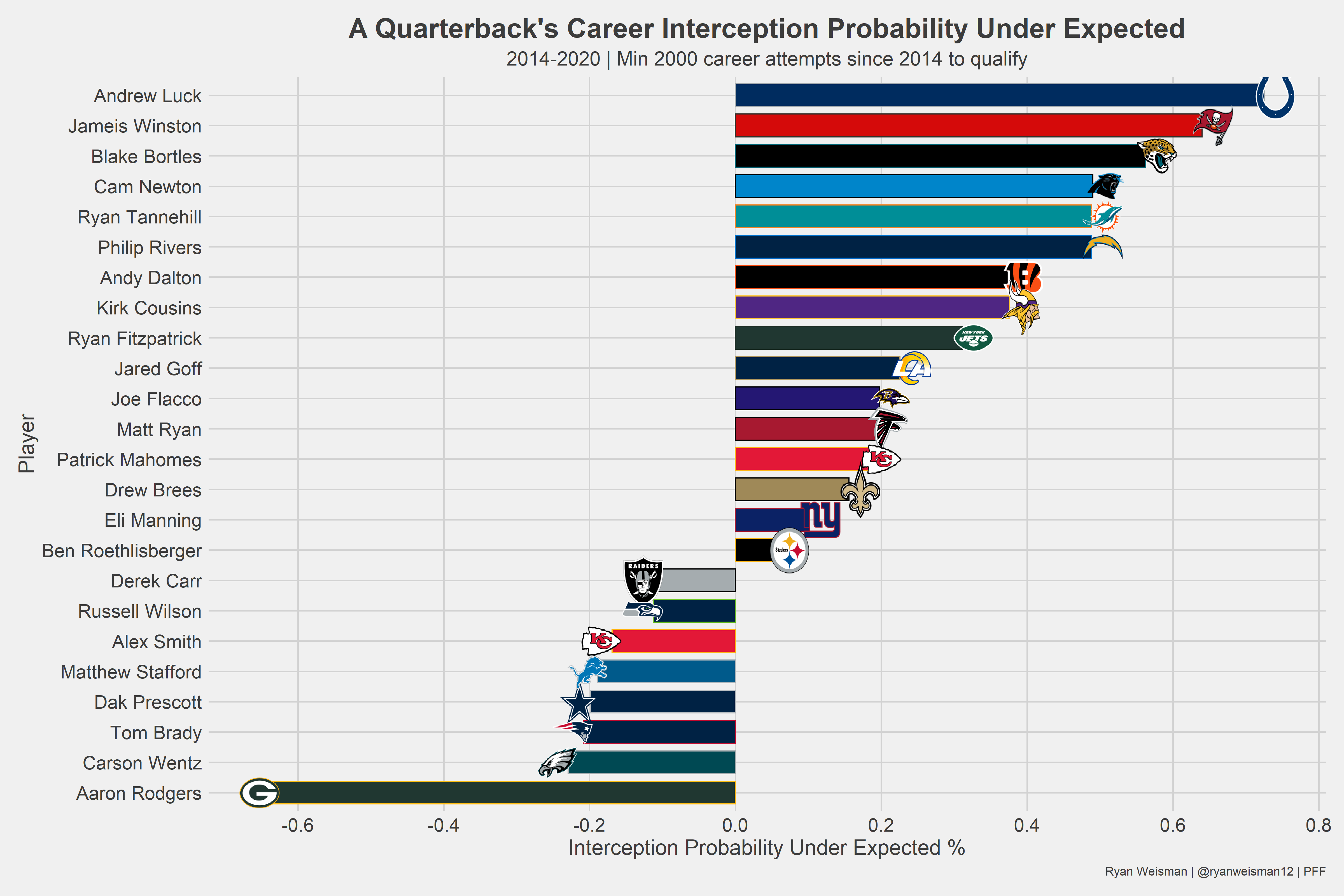
Andrew Luck is the unluckiest quarterback while Jameis Winston follows as a close second.
In addition to many other uses, interception probability can quantify luck in terms of a quarterback's interception rate, which allows us to better evaluate their play. A limitation to this statistic is that it does not explain why a quarterback is lucky. It can identify if they are/aren’t, but additional research is required to figure out the reason behind it.
Let’s look at quarterbacks in 2021.
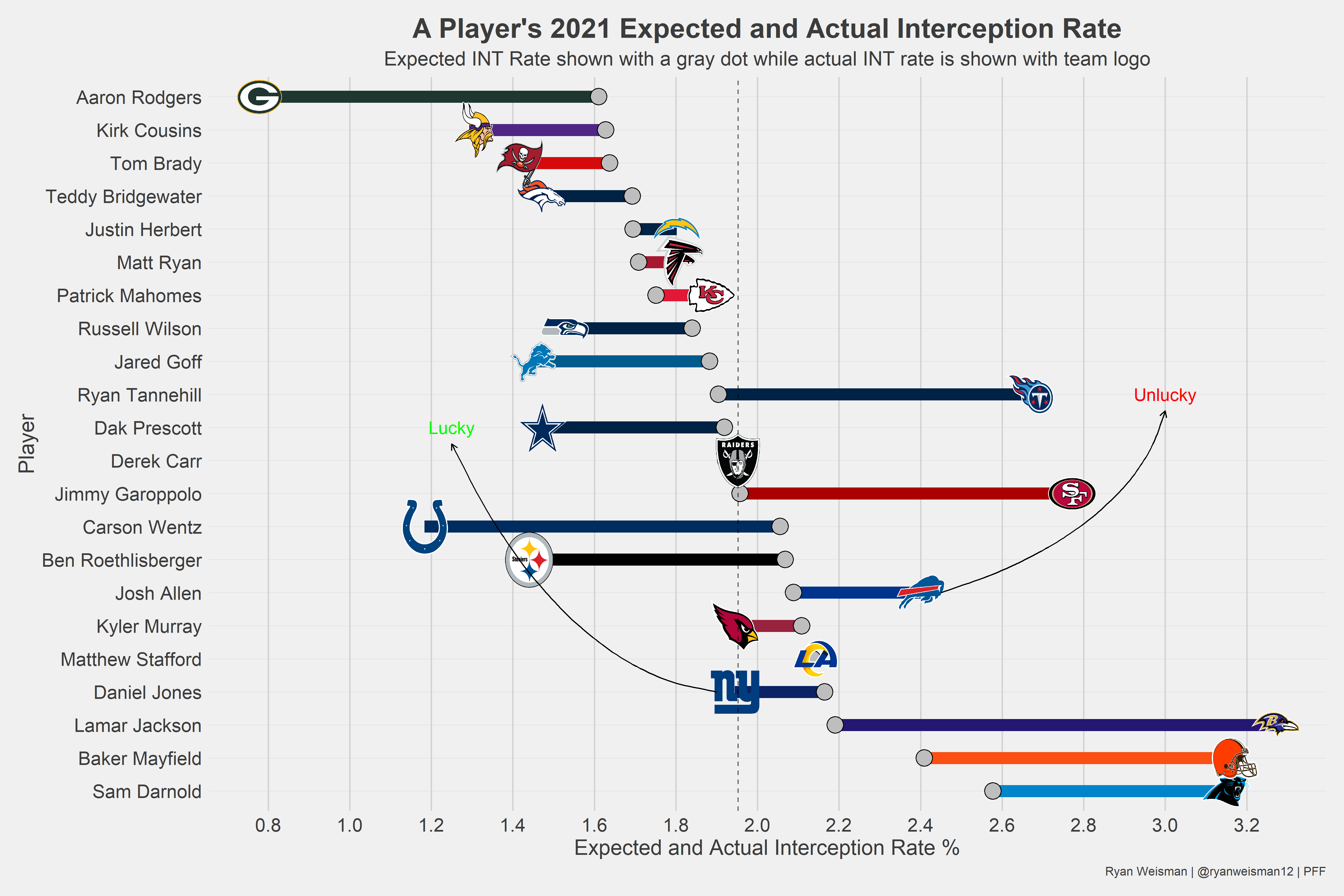
Even in 2021, Rodgers is still, by far, the luckiest quarterback. Lamar Jackson and Jimmy Garoppolo were incredibly unlucky.
This proposes a question: Rodgers is super lucky both in his career and 2021, does that mean this metric carries over from one year to the next?
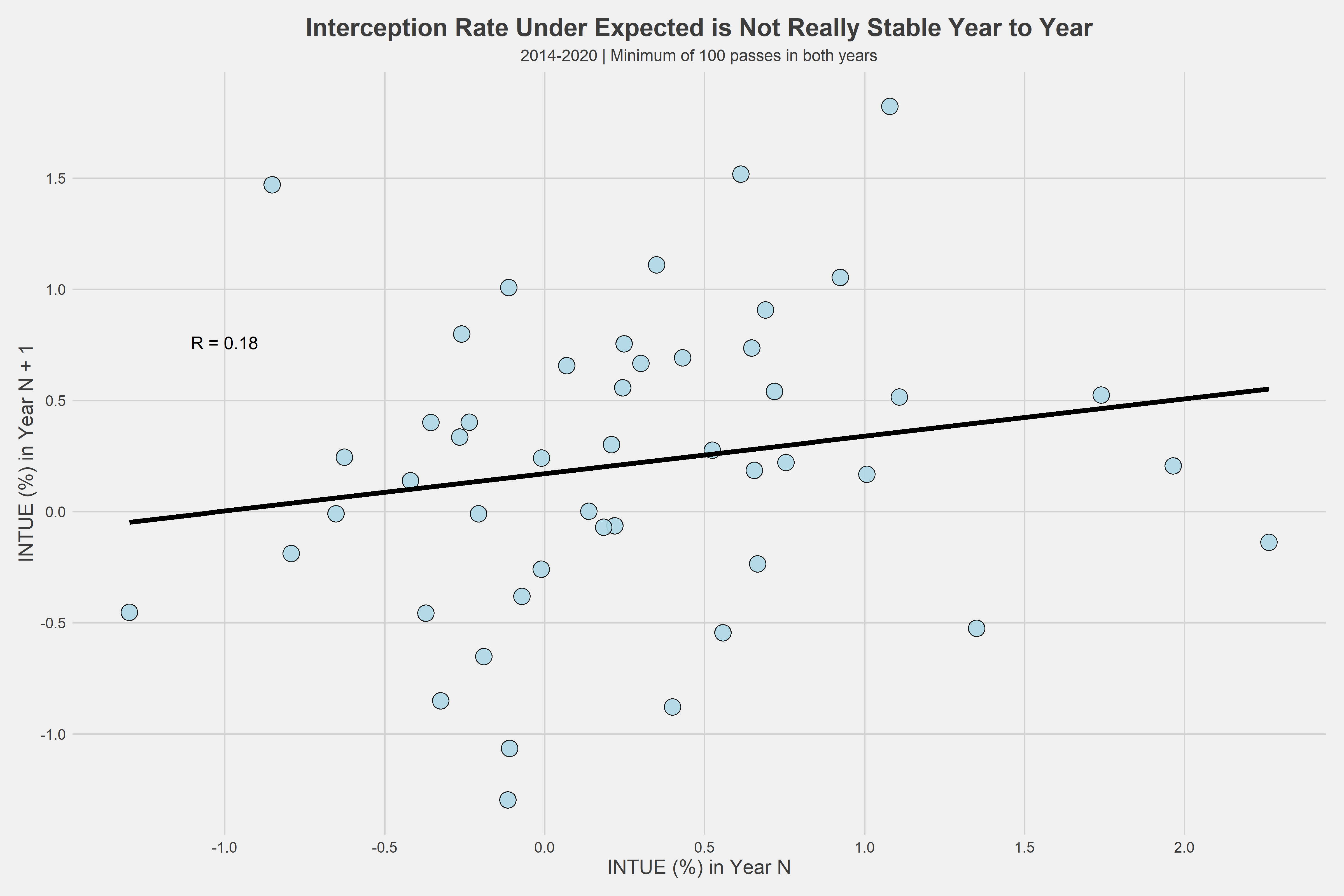
No, not particularly. Interception Rate Under Expected (INTUE) is not stable year to year. This makes sense, as luck is not consistent, hence the phrase regression to the mean. What this means is a quarterback who was really lucky one season is not likely to be as lucky the next. In addition, there is so much randomness during a football play that could cause an interception.
It makes sense INTUE is not stable year to year because a lot of luck is involved. However, it’s important to see if our expected interception probability model is stable year to year, as the actual expected probabilities are not luck-based.
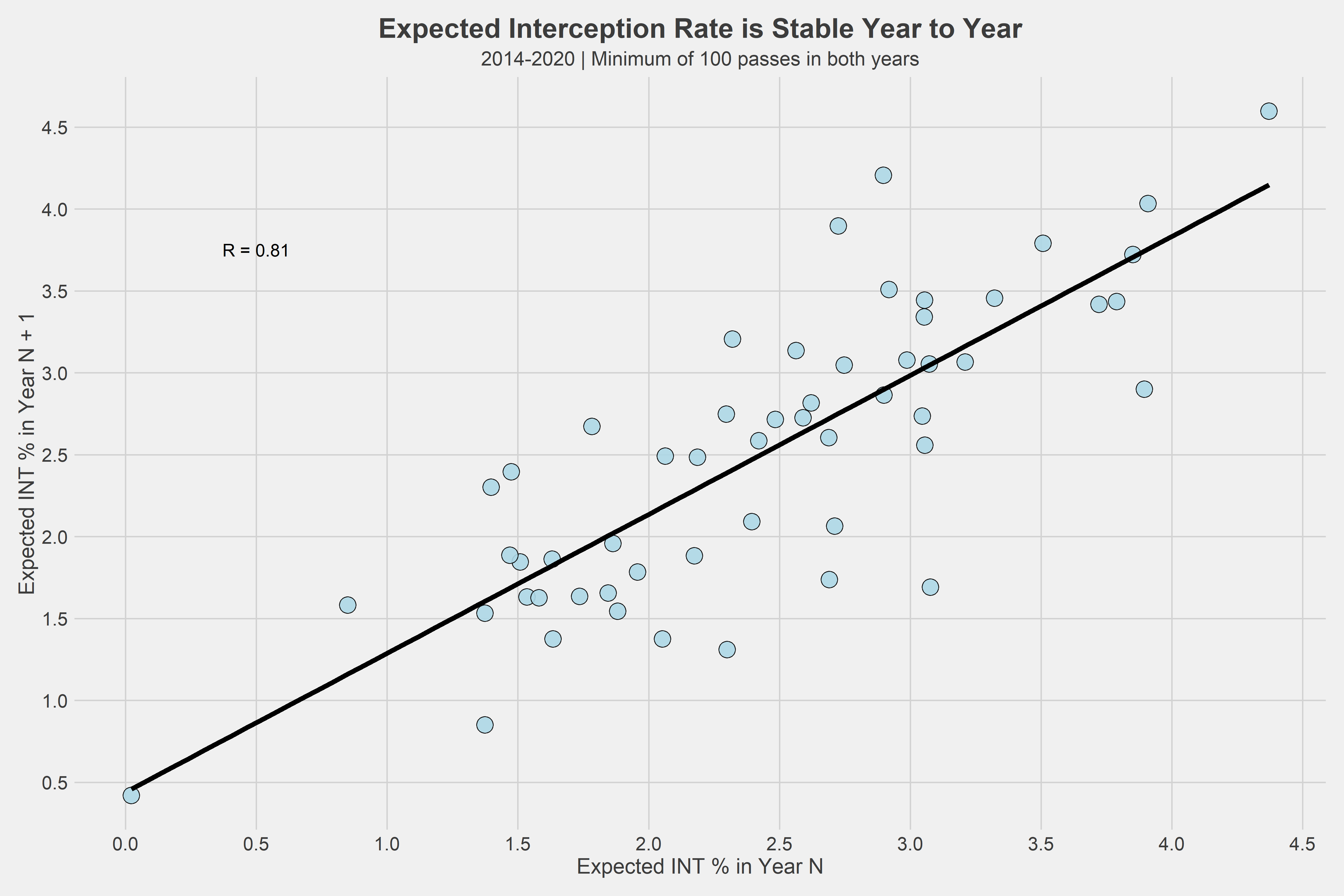
We can see that it is stable, which makes a lot of sense. A quarterback who has a low expected interception rate in one year will likely have a low expected interception rate in the next, though what will not be consistent is his actual interception rate, as many random variables affect that. The model adjusts for these variables, and this is the beauty of expected interception probability.
PFF has another metric that determines the rate at which a quarterback commits a turnover-worthy play called turnover worth play percentage (TWP%). We can use this to see if a quarterback’s interception probability under expected (INTUE) correlates with TWP%.
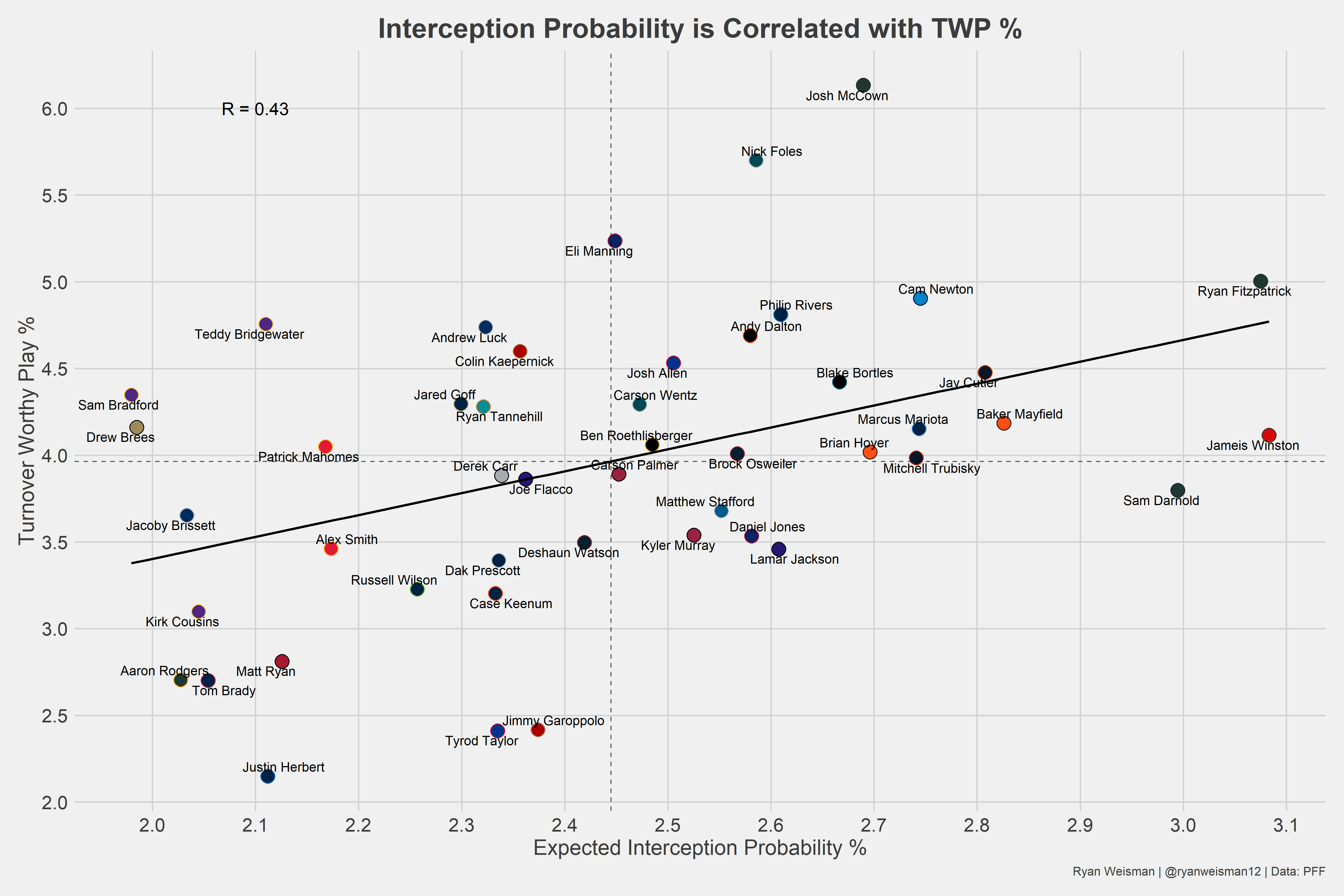
There is some correlation between the two variables. You’ll notice, in general, quarterbacks who have a high expected interception rate also have a high TWP%. This tells us our expected interception model is pretty good and allows us to create accurate deviations between a quarterback’s actual interception rate and their expected one.
The final question to ask: Does a quarterback’s interception probability under expected correlate with their success?
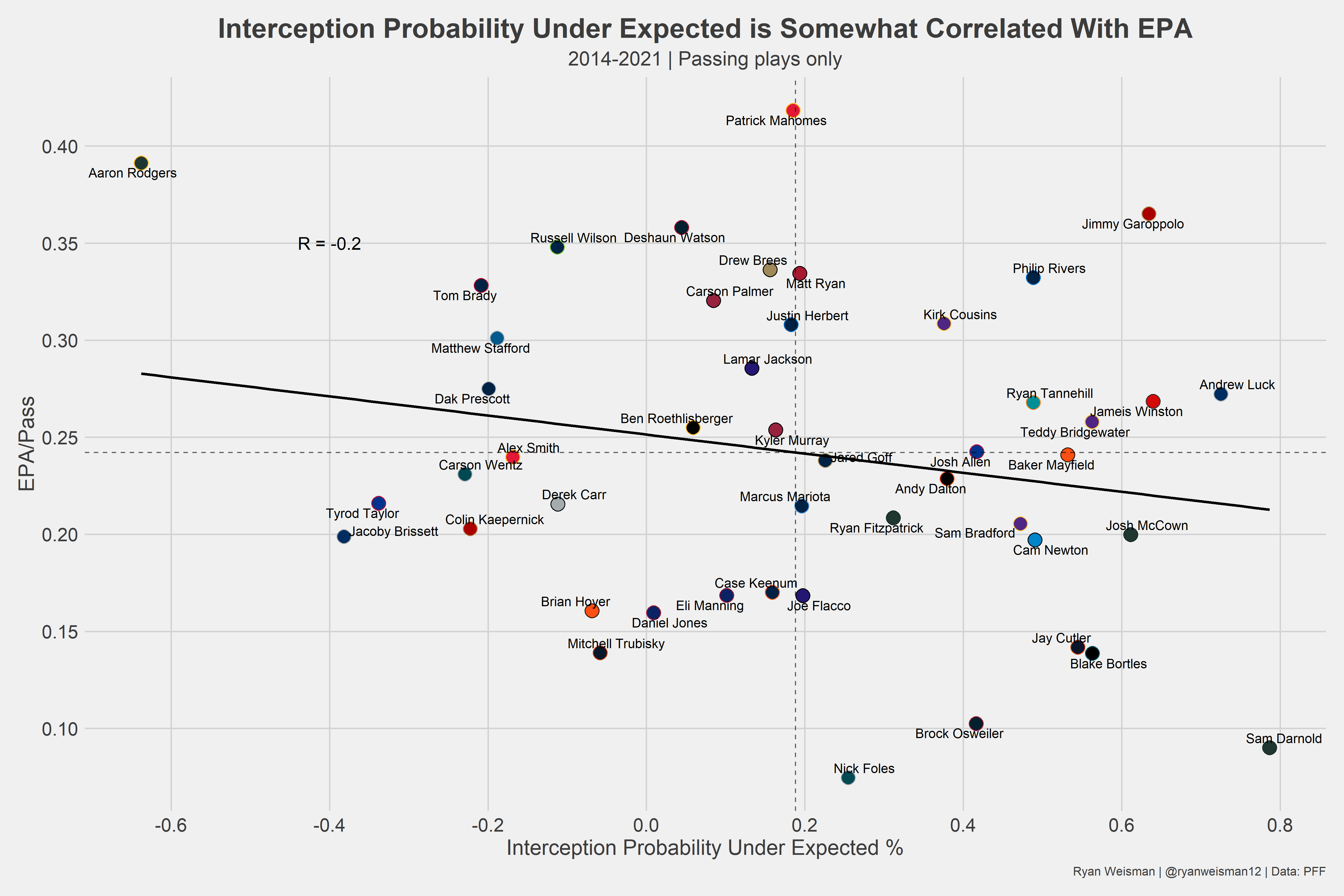Kind of. Keep in mind that this is only a quarterback’s success on valid passing plays. Luck is random, so it makes sense why a quarterback’s career EPA barely correlates with their interception luck.
Interception probability provides an excellent way to evaluate a quarterback’s performance. You obviously can’t generalize a quarterback’s success simply based on their interception probability under expected — as shown by the EPA figure — but you can weigh interception probability as an accurate facet when evaluating QBs.
We can now see that sure, Rodgers has been incredibly lucky when it comes to his passes not being picked off; however, his expected interception rate is still very low. With MVP voting coming up, some may argue Rodgers’ luck is a reason he is so high in the rankings, so he should be ranked lower, but his expected interception rate is still so low.
Last summer, I built another model with Ryan Brill, a PhD student from the University of Pennsylvania, where we aimed to predict the next NFL MVP. Below are the chances we think each QB has to win the MVP.
https://twitter.com/ryanweisman12/status/1481743770202689537?s=20
You’ll notice that Rodgers has the highest chance. He only has four interceptions, but that is attributed to luck. Should he have more? Yes. Though, the potential increase wouldn't be enough to make a case against him, as he is simply lucky due to his low expected interception rate.
This is yet another application of interception probability. It allows us to adjust for these confounding variables and truly evaluate a quarterback’s interception rate.
Interceptions are an incredibly important part of the game. Since 2014, the average EPA an interception has cost is -4.34, which is huge. You want quarterbacks to throw as few interceptions as possible, but a quarterback’s raw interception rate is very convoluted. There are so many confounding variables when it comes to looking at raw interception rate, such as an interception being dropped or a hail mary.
The model aims to adjust for these factors as best as possible.
© 2024 PFF - all rights reserved.